Operations Research: a supply chain perspective
Background
Operations Research (OR) deals with the efficient allocation of scarce resources and is regarded as the discipline that applies advanced analytical methods to help improve decision making. It originated the 1930s by military scientists who developed many analyses that were crucial to the war effort. Following the war, these techniques were applied to problems in business, industry, government and society. Strictly speaking, OR is not a science per se – rather, it overlaps with other disciplines and is a consolidation of analytical methods and models that we sometimes refer to as applied decision theory.
There are many interesting definitions, notably;
“The art of giving bad answers to problems which otherwise have worse answers” (T.L. Saaty), and
“The art of winning wars without actually fighting them” (Arthur Clarke)
Following the emergence of modern computing technologies, OR increasingly gained in popularity, in particular within the field of supply chain management where often we encounter many optimisation problems with conflicting objectives. In today’s supply chain, most of the problems tackled by OR can be messy and complex, often involving considerable uncertainty.
This requires the use of advanced optimisation techniques, modelling, and simulation to determine the best solutions and estimates of risk that ultimately lead to a recommended course of action. Depending on the problem, the benefits of OR generally address performance improvements in cost reduction, revenue enhancement, service levels, inventory control, activity scheduling, and so on.
Interestingly, OR is formally recognised as one of the sixty-four mathematical disciplines and this particular category (90B) is further classified into eighteen specific research areas, all closely linked to supply chain; some examples are:
90B05 Inventory and Storage
90B06 Transportation and Logistics
90B15 Stochastic Network Models
90B80 Discrete Location and Assignment
In a situation where there is a need to optimise, decisions must be made to achieve the best value of the constrained objective (otherwise, everything will be achievable!). Fortunately, many supply chain problems are amenable to treatment using mathematical programming techniques and likewise, this is also a subject in its own right (assigned category 90C).
Over the coming months, we shall present a series of examples typifying the links between OR and the supply chain. To begin, one of the most important and successful applications we often encounter is the physical distribution of products, commonly referred to as the transportation problem.
The Transportation Problem
The basic purpose is to minimise the distribution costs from one location to another so that the demands of each destination (e.g. customer) are satisfied and every source location (e.g. plant) operates within its capacity. Such problems arise in situations involving the physical movement of goods from plants to warehouses, warehouses to warehouses, wholesalers to retailers and retailers to customers.
Each model requires three components – variables to represent decisions to be made, constraints to restrict the values of these decision variables and an objective function to express the performance measure of the problem. We must also consider the numerical methods required to solve the problem.
Typically, the transportation problem is solved using a mixed integer programme in which the objective function is set to minimise the overall distribution costs for all source-destination combinations. Further, the constraints ensure that the capacity at each facility is not breached and that demand at each location is satisfied.
In setting-up the model, we must quantify
- The supply at each source and the demand for each destination, and
- The unit transportation cost of the commodity from each source to each destination
Transportation problems may be either balanced (where supply matches demand) or unbalanced (in which case, demand exceeds supply or vice versa). For the latter, we can recast the formulation by assigning a dummy destination or source.
Optimisation problems of moderate-scale can be formulated by the supply chain practitioner and solved rapidly using the Simplex LP functionality in Excel© Solver. The output of the spreadsheet model provides a solution that minimises the total shipping costs from the production plants to all demand destinations (customers or warehouses, or both). Larger scale problems will require more complex toolsets and some variation in the mathematical techniques used, but the principles behind the optimisation approach are similar.
Case Study
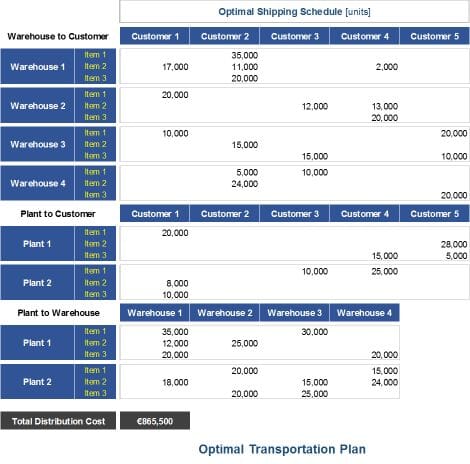
Let us suppose that a company produces 3 commodities in 2 separate manufacturing locations. Finished goods are either despatched directly to 5 customer regions or across a network of 4 DCs, separated geographically. This company requires a shipment plan that satisfies the total customer demand at the minimum distribution cost. Products may be shipped in combinations of plants to warehouses, plants to customers, and warehouses to customers.
Multi-stage, multi-commodity transportation problem
as in this example, requires information on unit shipment costs across the network nodes (which is easy to determine using location data, etc.) and, provided the demand for each product is assigned to each customer region, then once the appropriate constraints are imposed, the recommended shipment schedule can be determined using linear programming algorithms.
For this particular example, the optimal solution generated minimises the transportation cost (€865.5k) by distributing each commodity to the customer base in accordance with the allocation shown. Using this spreadsheet model, we can easily verify that both plant and warehouse capacities are not exceeded, and that customer demand is fully satisfied (for the interested reader, the model formulations are available on request).
This is one brief illustration of a simplified optimisation problem that can be solved without the need for extensive capital investment or specialised resources. No doubt, spreadsheets are very capable decision tools and although they have more limitations (for iterative calculations) compared to some of the standalone optimisation systems that we use, we find that applied appropriately, they help increase understanding of optimisation trade offs and can have a role in solving many of today’s supply chain problems.
Next month, we will introduce another fundamental OR application; the so-called assignment problem. Here, for example, you can see how work and resources in an order picking process can be efficiently allocated.
Meanwhile, if you have any questions, or further interest in any aspect of supply chain optimisation, please contact us.
Supply Chain Enabled
